Tutorial 2: Double descent

Tutorial 2: Double descent#

Week 2, Day 1: Macrocircuits

By Neuromatch Academy

Content creators: Andrew Saxe, Vidya Muthukumar

Content reviewers: Max Kanwal, Surya Ganguli, Xaq Pitkow, Hlib Solodzhuk, Patrick Mineault

Production editors: Konstantine Tsafatinos, Ella Batty, Spiros Chavlis, Samuele Bolotta, Hlib Solodzhuk

Tutorial Objectives#

Estimated timing of tutorial: 1 hour

In this tutorial, we’ll look at the sometimes surprising behavior of large neural networks, which is called double descent. This empirical phenomenon puts the classical understanding of the bias-variance tradeoff in question: in double descent, highly overparametrized models can display good performance. In particular, we will explore the following:

notions of low/high bias/variance;
improvement of test performance with the network’s overparameterization, which leads to large model trends;
the conditions under which double descent is observed and what affects its significance;
the conditions under which double descent does not occur.

Let’s jump in!

Setup#

Install and import feedback gadget#

Imports#

Figure settings#

Plotting functions#

Helper functions#

Show code cell source Hide code cell source

# @title Helper functions

def sin_dataset(sigma = 0):
    """
    Create a sinusoidal dataset and sample 10 points from it for a training dataset.
    Training set incorporates Gaussian noise added to the target values of the given standard deviation.

    Inputs:
    - sigma (float, default = 0): standard deviation of the train noise.

    Outputs:
    - x_train, y_train, x_test, y_test (tuple of np.ndarray): train and test data.
    """

    # Create a sinusoidal dataset and sample 10 points from it for a training dataset
    x_test = np.linspace(-np.pi, np.pi, 100)
    y_test = np.sin(x_test)

    x_train = np.linspace(-np.pi, np.pi, 10)
    # y_train = np.sin(x_train) + 0.05 * np.random.normal(size=10)
    y_train = np.sin(x_train) + sigma * np.random.normal(size=10)

    return x_train.reshape(10,1), y_train.reshape(10,1), x_test.reshape(100,1), y_test.reshape(100,1)

def fit_relu_implemented(x_train, y_train, x_test, y_test, n_hidden = 10, reg = 0):
    """
    Fit the second layer of the network by solving via linear regression for the given training data and evaluate the performance.

    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - n_hidden (int, default = 10): the size of the hidden layer.
    - reg (float, default = 0): regularization term.

    Outputs:
    - train_err (float): train error value.
    - test_err (float): test error value.
    - y_pred (np.ndarray): array of predicted values for test data.
    """

    # Define network architecture
    n_inputs = 1  # Number of input features
    n_outputs = 1  # Number of output units

    # Layer 1 (Input -> Hidden)
    W1 = np.random.normal(0, 1, (n_inputs, n_hidden))  # Random weights
    b1 = np.random.uniform(-np.pi, np.pi, size = (1, n_hidden))  # Bias

    # Layer 2 (Hidden -> Output)
    W2 = np.zeros((n_hidden, n_outputs))  # Initialize weights to zero

    # Forward propagation
    def forward_prop(X):
        z1 = X.dot(W1) + b1
        a1 = np.maximum(0, z1)  # ReLU activation
        z2 = a1.dot(W2)
        return z2

    # Fit second layer weights with linear regression
    hidden = np.maximum(0, x_train.dot(W1) + b1)  # Hidden layer activations
    if reg == 0:
        # Pseudo-inverse solution
        hidden_pinv = np.linalg.pinv(hidden)
        W2 = hidden_pinv.dot(y_train)
    else:
        # We use linalg.solve to find the solution to (H'H + reg*I) * W2 = H'y,
        # equivalent to W2 = (H'H + reg*I)^(-1) * H'y
        W2 = np.linalg.solve(hidden.T @ hidden + reg * np.eye(n_hidden), hidden.T @ y_train)

    # Train Error
    y_pred = forward_prop(x_train)
    train_err = np.mean((y_train-y_pred)**2/2)

    # Test Error
    y_pred = forward_prop(x_test)
    test_err = np.mean((y_test-y_pred)**2/2)

    return train_err, test_err, y_pred


def fit_relu_init_scale(x_train, y_train, x_test, y_test, init_scale = 0, n_hidden = 10, reg = 0):
    """
    Fit the second layer of the network by solving for linear regression with pseudo-inverse for the given training data and evaluate the performance on test one.

    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - init_scale (float, default = 0): initial standard deviation for weights in the second layer.
    - n_hidden (int, default = 10): the size of the hidden layer.
    - reg (float, default = 0): regularization term.

    Outputs:
    - train_err (float): train error value.
    - test_err (float): test error value.
    - y_pred (np.ndarray): array of predicted values for test data.
    """

    # Define network architecture
    n_inputs = 1  # Number of input features
    n_outputs = 1  # Number of output units

    # Layer 1 (Input -> Hidden)
    W1 = np.random.normal(0,1, (n_inputs, n_hidden))  # Random weights
    b1 = np.random.uniform(-np.pi, np.pi, size=(1, n_hidden))  # Bias

    # Layer 2 (Hidden -> Output)
    W2 = np.random.normal(0,init_scale,(n_hidden, n_outputs))  # Initialize weights to zero

    # Forward propagation
    def forward_prop(X):
        z1 = X.dot(W1) + b1
        a1 = np.maximum(0, z1)  # ReLU activation
        z2 = a1.dot(W2)
        return z2

    # Fit second layer weights with linear regression
    hidden = np.maximum(0, x_train.dot(W1) + b1)  # Hidden layer activations
    if reg == 0:
        hidden_pinv = np.linalg.pinv(hidden)
        W2 = hidden_pinv.dot(y_train) + (np.eye(n_hidden) - hidden_pinv @ hidden) @ W2   # Pseudo-inverse solution plus component in data nullspace
    else:
        hidden_pinv = np.dot(np.linalg.pinv(np.dot(hidden.T, hidden) + reg*np.eye(n_hidden)), hidden.T)
        W2 = hidden_pinv.dot(y_train) + (np.eye(n_hidden) - hidden_pinv @ hidden) @ W2   # Pseudo-inverse solution plus component in data nullspace

    # Train Error
    y_pred = forward_prop(x_train)
    train_err = np.mean((y_train-y_pred)**2/2)

    # Test Error
    y_pred = forward_prop(x_test)
    test_err = np.mean((y_test-y_pred)**2/2)

    return train_err, test_err, y_pred

def sweep_test_init_scale(x_train, y_train, x_test, y_test, init_scale = 0, n_hidden = 10, n_reps = 20):
    """
    Calculate the mean test error for fitting the second layer of the network for a defined number of repetitions.
    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - init_scale (float, default = 0): initial standard deviation for weights in the second layer.
    - n_hidden (int, default = 10): size of hidden layer.

    Outputs:
    - (float): mean error for test data.
    """
    return np.mean(np.array([fit_relu_init_scale(x_train, y_train, x_test, y_test, init_scale=init_scale, n_hidden=n_hidden)[1] for i in range(n_reps)]))

def sweep_train(x_train, y_train, x_test, y_test, n_hidden = 10, n_reps = 20):
    """
    Calculate the mean train error for fitting the second layer of the network for a defined number of repetitions.
    Notice that `init_scale` is always set to be 0 in this case.
    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - n_hidden (int, default = 10): size of hidden layer.

    Outputs:
    - (float): mean error for train data.
    """
    return np.mean(np.array([fit_relu(x_train, y_train, x_test, y_test, n_hidden=n_hidden)[0] for i in range(n_reps)]))

Set random seed#

Video 1: Introduction#

Submit your feedback#

Section 1: Overfitting in overparameterized models#

In this section we will observe the classical behaviour of overparametrized networks - overfitting.

Video 2: Overfitting in Overparameterized Models#

Submit your feedback#

Coding Exercise 1: Learning with a simple neural network#

We start by generating a simple sinusoidal dataset.

This dataset contains 100 datapoints. We’ve selected a subset of 10 points for training.

Sample and plot sinusoidal dataset#

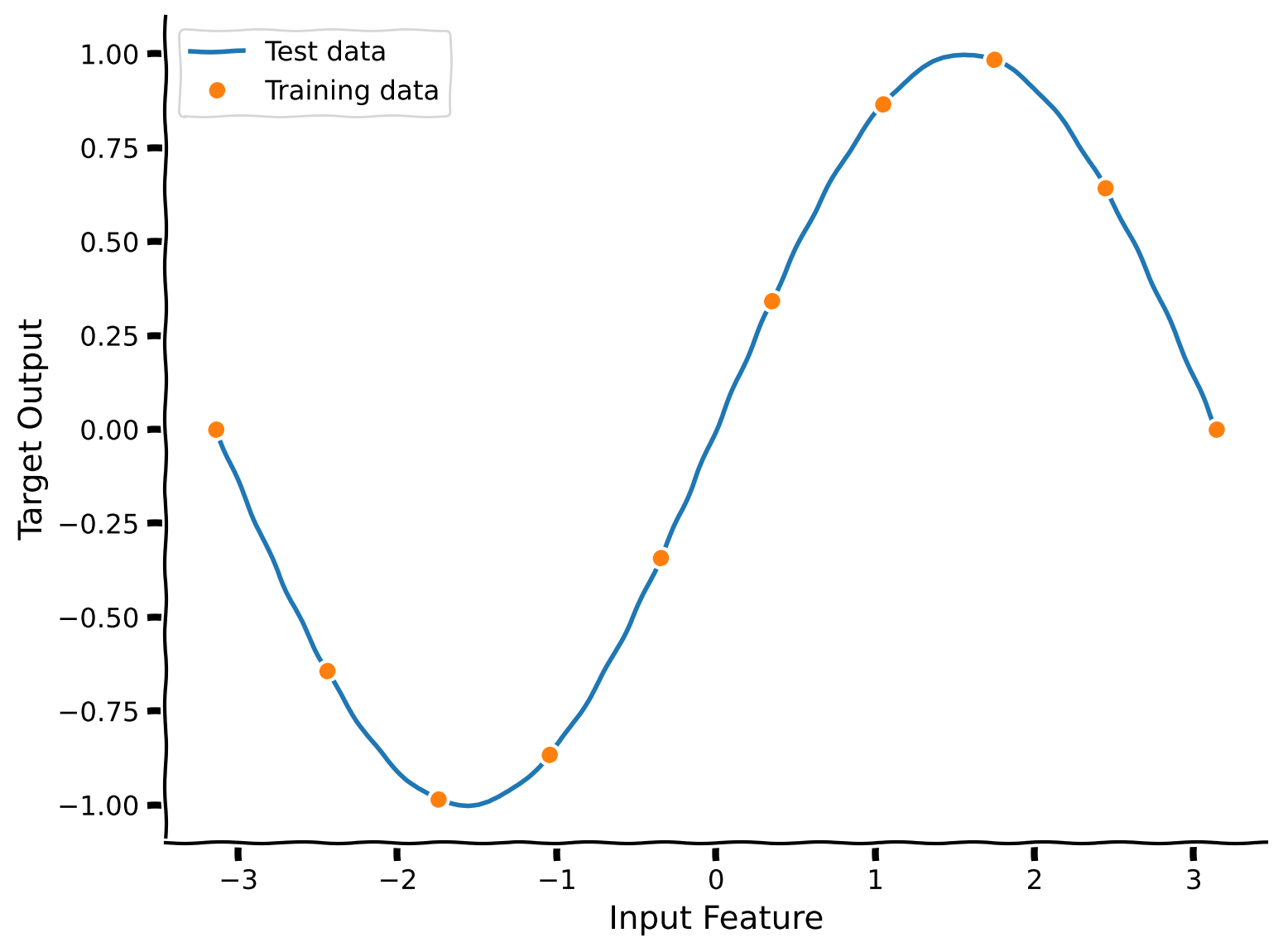
../../../_images/5dd3047a0cbd7a0cb76be88f114f01a548c97a08506de279d8c9dd2f35fc8d13.png

We’ll learn this task with a simple neural network: a one-hidden-layer ReLU network, where the first layer is fixed and random.

That is, the network computes its hidden activity as \(h = ReLU(W_1x + b)\), and its output as \(\hat y = W_2h\).

The input \(x\in R\) is a scalar. There are \(N_h\) hidden units, and the output \(\hat y\in R\) is a scalar.

We will initialize \(W_1\) with i.i.d. random Gaussian values with a variance of one and \(b\) with values drawn i.i.d. uniformly between \(-\pi\) and \(\pi\). Finally, we will initialize the weights \(W_2\) to zero.

We only train \(W_2\), leaving \(W_1\) and \(b\) fixed. We can train \(W_2\) to minimize the mean squared error between the training labels \(y\) and the network’s output on those datapoints.

Usually, we would train this network using gradient descent, but here, we’ve taken advantage of the fixed first layer to compute the solution in closed form using linear regression. This is much faster than gradient descent, allowing us to us rapidly train many networks.

Closed-form solution derivation (optional)

To find \(W_2\), we will rewrite the problem in matrix form. Let:

\(X\) be the matrix of input data (shape \( n \times 1 \))
\(H\) be the matrix of hidden activations after ReLU (shape \( n \times N_h \))
\(y\) be the vector of target outputs (shape \(n \times 1\))

\(W_1\), \(W_2\) and \(b\) are of shape \(N_h \times 1\).

Compute the hidden activations:

\[ H = \text{ReLU}(X W_1^\top + b) \]

The predicted outputs can be written as:

\[ \hat{y} = H W_2 \]

We aim to minimize the mean squared error (MSE) between the predicted output \(\hat{y}\) and the true output \(y\):

\[ \mathcal{L} = \text{MSE} = (H W_2 - y)^2 \]

By taking the derivative of this expression by \(W_2\), we get:

\[ \frac{\partial \mathcal{L}}{\partial W_2} = 0 = 2H^\top HW_2 - 2H^\top y \]

Meaning that the optimal solution \(W_2\) is:

\[ W_2 = H^+ y \]

Here, \(H^+\) is the Moore-Penrose pseudoinverse.

Below is the skeleton code for this network. Your task is to implement its weight initialization and forward pass function. In the cell below, you can test your solution.

def fit_relu(x_train, y_train, x_test, y_test, n_hidden = 10, reg = 0):
    """
    Fit the second layer of the network by solving via linear regression for the given training data and evaluate the performance.

    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - n_hidden (int, default = 10): the size of the hidden layer.
    - reg (float, default = 0): regularization term.

    Outputs:
    - train_err (float): train error value.
    - test_err (float): test error value.
    - y_pred (np.ndarray): array of predicted values for test data.
    """

    # Define network architecture
    n_inputs = 1  # Number of input features
    n_outputs = 1  # Number of output units

    ###################################################################
    ## Fill out the following, then remove
    raise NotImplementedError("Student exercise: complete initialization of layers as well as forward propagation for the network (follow the description in the text above).")
    ###################################################################

    # Layer 1 (Input -> Hidden)
    W1 = np.random.normal(0, ..., (n_inputs, ...))  # Random weights
    b1 = np.random.uniform(-np.pi, ..., size = (1, n_hidden))  # Bias

    # Layer 2 (Hidden -> Output)
    W2 = np.zeros((..., ...))  # Initialize weights to zero

    # Forward propagation
    def forward_prop(X):
        z1 = X.dot(...) + ...
        a1 = np.maximum(0, ...)  # ReLU activation
        z2 = a1.dot(...)
        return z2

    # Fit second layer weights with linear regression
    hidden = np.maximum(0, x_train.dot(W1) + b1)  # Hidden layer activations
    if reg == 0:
        # Pseudo-inverse solution
        hidden_pinv = np.linalg.pinv(hidden)
        W2 = hidden_pinv.dot(y_train)
    else:
        # We use linalg.solve to find the solution to (H'H + reg*I) * W2 = H'y,
        # equivalent to W2 = (H'H + reg*I)^(-1) * H'y
        W2 = np.linalg.solve(hidden.T @ hidden + reg * np.eye(n_hidden), hidden.T @ y_train)

    # Train Error
    y_pred = forward_prop(x_train)
    train_err = np.mean((y_train-y_pred)**2/2)

    # Test Error
    y_pred = forward_prop(x_test)
    test_err = np.mean((y_test-y_pred)**2/2)

    return train_err, test_err, y_pred

Click for solution

Submit your feedback#

Coding Exercise 2: The bias-variance tradeoff#

With the network implemented, we now investigate how the size of the network (the number of hidden units it has, \(N_h\)) relates to its ability to generalize.

Ultimately, the true measure of a learning system is how well it performs on novel inputs, that is, its ability to generalize. The classical story of how model size relates to generalization is the bias-variance tradeoff.

To start, complete the code below to train several small networks with just two hidden neurons and plot their predictions.

set_seed(42)

n_hid = 2

n_reps = 10 # Number of networks to train

def plot_predictions(n_hid, n_reps):
    """
    Generate train and test data for `n_reps` times, fit it for a network with hidden size `n_hid`, and plot prediction values.

    Inputs:
    - n_hid (int): size of hidden layer.
    - n_reps (int): number of data regenerations.
    """
    with plt.xkcd():
        plt.plot(x_test, y_test,linewidth=4,label='Test data')
        plt.plot(x_train, y_train,'o',label='Training data')

        train_err, test_err, y_pred = fit_relu(x_train, y_train, x_test, y_test, n_hidden=n_hid)
        plt.plot(x_test, y_pred, color='g', label='Prediction')

        for rep in range(n_reps-1):
            ###################################################################
            ## Fill out the following then remove
            raise NotImplementedError("Student exercise: complete generation of new train / test data and visualize it.")
            ###################################################################
            train_err, test_err, y_pred = ...
            plt.plot(..., ..., color='g', alpha=.5, label='_')

        plt.legend()
        plt.xlabel('Input Feature')
        plt.ylabel('Target Output')
        plt.title('Number of Hidden Units = {}'.format(n_hid))
        plt.show()

plot_predictions(n_hid, n_reps)

Click for solution

Example output:

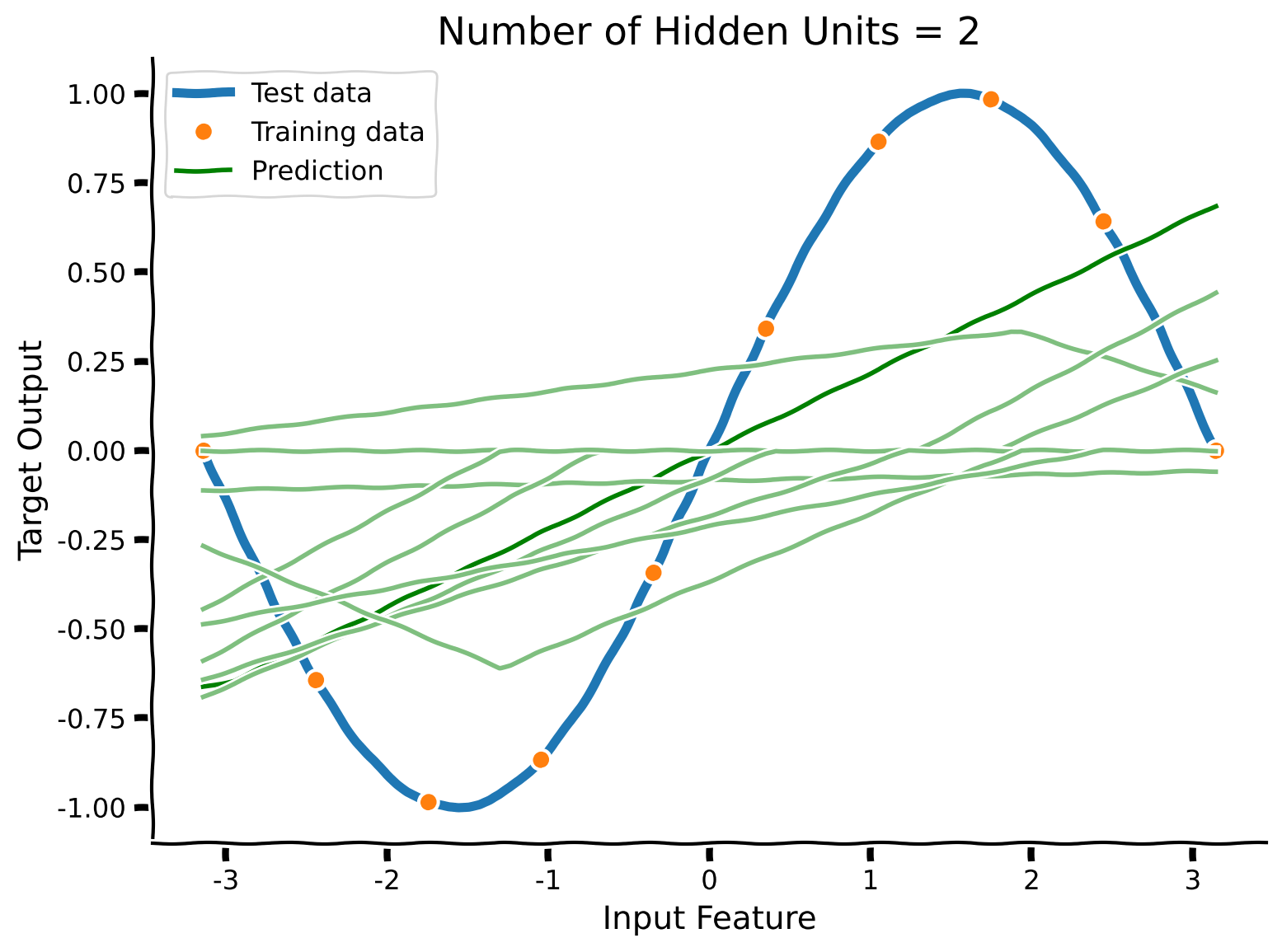
With just two hidden units, the model cannot fit the training data, nor can it do well on the test data. A network of this size has a high bias.

Now, let’s train a network with five hidden units.

Coding Exercise 2 Discussion#

Do you expect the network to fit the data better with five hidden units than with two units? Check your intuition by running the cell below.

Observe the performance on 5 hidden units#

With five hidden units, the model can do a better job of fitting the training data, and also follows the test data more closely - though still with errors.

Next let’s try 10 hidden units.

Observe the performance on 10 hidden units#

With 10 hidden units, the network often fits every training datapoint, but generalizes poorly–sometimes catastrophically so. We say that this size network has high variance. Intuitively, it is so complex that it can fit the training data perfectly, but this same complexity means it can take many different shapes in between datapoints.

We have just traced out the bias-variance tradeoff: the models with 2 hidden units had high bias, while the models with 10 hidden units had high variance. The models with 5 hidden units struck a balance–they were complex enough to achieve relatively low error on the training datapoints, but simple enough to be well constrained by the training data.

Submit your feedback#

Section 2: The modern regime#

Estimated timing to here from start of tutorial: 20 minutes

In this section, we will go beyond ten hidden units, which might sound unreasonable, but it will result in an unexpected plot twist.

Video 3: Modern Regime#

Submit your feedback#

We just saw that a network with 10 hidden units trained on 10 training datapoints could fail to generalize. If we add even more hidden units, it seems unlikely that the network could perform well. How could hundreds of weights be correctly constrained with just these ten datapoints?

But let’s try it. Throw caution to the wind and train a network with 500 hidden units.

Observe the performance on 500 hidden units#

Coding Exercise 3: Observing double descent#

Remarkably, this very large network fits the training datapoints and generalizes well.

This network has fifty times as many parameters as datapoints. How can this be?

We’ve tested four different network sizes and seen the qualitative behavior of the predictions. Now, let’s systematically compute the average test error for different network sizes.

For each network size in the array below, train 100 networks and plot their mean test error.

set_seed(42)

n_hids = np.unique(np.round(np.logspace(0, 3, 20))).astype(int)

###################################################################
## Fill out the following then remove
raise NotImplementedError("Student exercise: complete calculation of mean test error for different sizes of hidden units defined above.")
###################################################################

def sweep_test(x_train, y_train, x_test, y_test, n_hidden = 10, n_reps = 100, reg = 0.0):
    """
    Calculate the mean test error for fitting the second layer of the network for a defined number of repetitions.
    Notice that `init_scale` is always set to 0 in this case.
    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - n_hidden (int, default = 10): size of hidden layer.
    - n_reps (int, default = 100): number of resamples for data.
    - reg (float, default = 0): regularization constant.

    Outputs:
    - (float): mean error for train data.
    """
    return np.mean(np.array([fit_relu(..., ..., ..., ..., n_hidden=n_hidden, reg = reg)[1] for _ in range(n_reps)]))

test_errs = [sweep_test(x_train, y_train, x_test, y_test, n_hidden=..., n_reps=100, reg = 0.0) for n_hid in ...]

with plt.xkcd():
    plt.loglog(n_hids,test_errs,'o-',label='Test')
    plt.xlabel('Number of Hidden Units')
    plt.ylabel('Test Error')
    plt.show()

Click for solution

Example output:

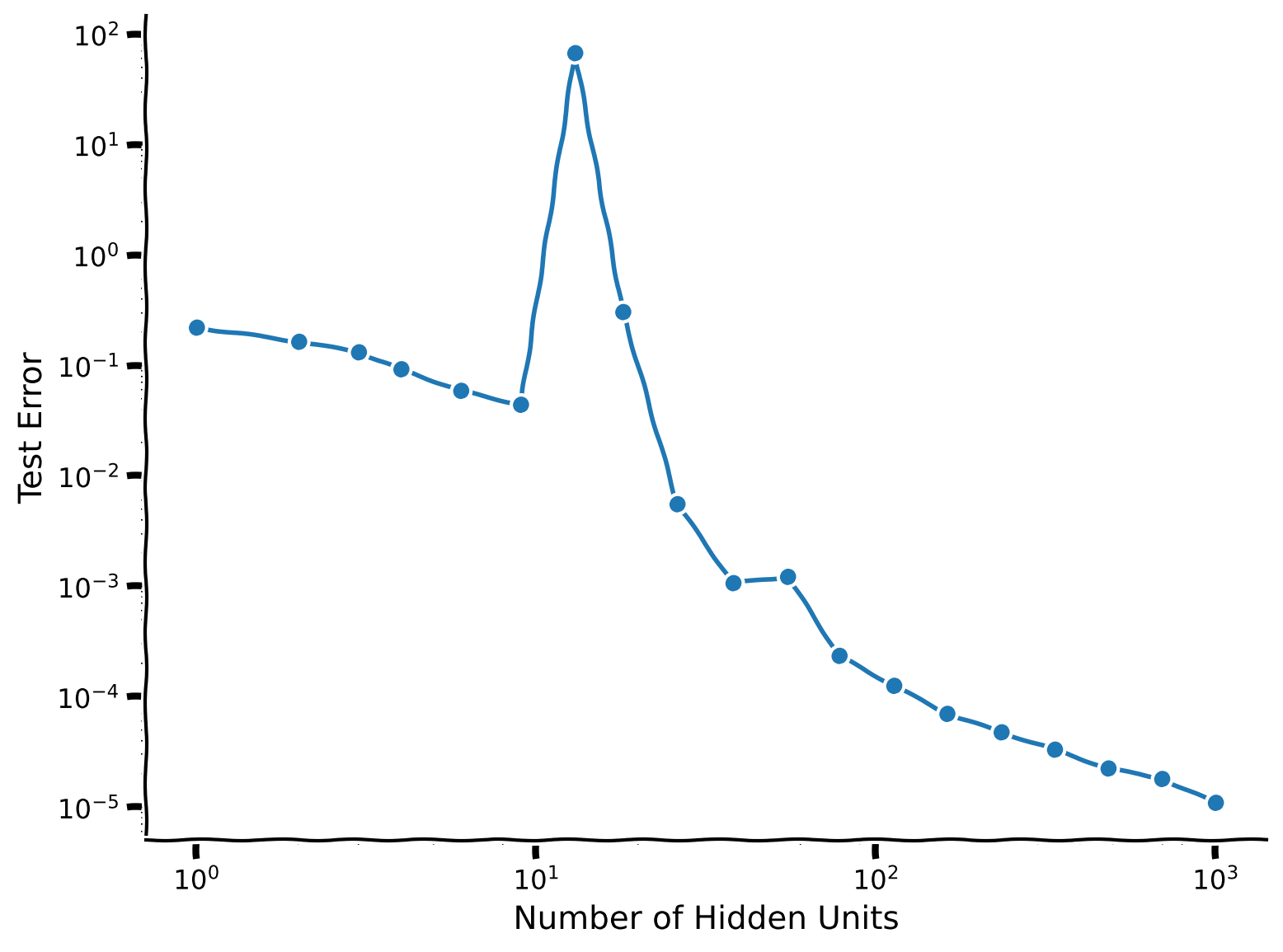
This curve is an example of the double descent phenomenon: between 1 hidden unit and 10 hidden units, we see the bias-variance tradeoff (containing the first descent). The test error reaches its peak at 10 hidden units. Then it descends again (hence double descent), eventually outperforming the smaller models.

Hence, in this scenario, larger models perform better–even when they contain many more parameters than datapoints.

The peak (worst generalization) is at an intermediate model size when the number of hidden units is equal to the number of examples in this case. More generally, it turns out the peak occurs when the model first becomes complex enough to reach zero training error. This point is known as the interpolation point.

The trend for deep learning models to grow in size is in part due to this phenomenon of double descent. Let’s now see its limits.

Interactive Demo 1: Interpolation point & predictions#

In this interactive demo, you can move the slider for the number of hidden units in the network to be trained on and observe one representative trial of predicted values.

Execute this cell to observe interactive plot#

The trend for deep learning models to grow in size is in part due to the phenomenon of double descent. Let’s now see its limits.

Submit your feedback#

Section 3: Double descent, noise & regularization#

Estimated timing to here from start of tutorial: 35 minutes

In this section, we are going to explore the effect of noise and regularization on double descent behavior.

Video 4: Noise & Regularization Effects#

Submit your feedback#

Coding Exercise 4: Noise & regularization impact#

So far, our training datapoints have been noiseless. Intuitively, a noisy training dataset might hurt the ability of complex models to generalize. In this section, we are going to explore the effect of noise on double descent behavior.

Let’s test this. Add i.i.d. Gaussian noise of different standard deviations to the training labels, and plot the resulting double descent curves.

set_seed(42)

n_hids = np.unique(np.round(np.logspace(0, 3, 10))).astype(int)

std_devs = np.linspace(0, 1.0, 3)

def plot_error(x_train, y_train, x_test, y_test, std_devs, n_hids, n_hidden = 10, n_reps = 100, reg = 0.0):
    """
    Plot mean test error for distinct values of noise added to train dataset.

    Inputs:
    - x_train (np.ndarray): train input data.
    - y_train (np.ndarray): train target data.
    - x_test (np.ndarray): test input data.
    - y_test (np.ndarray): test target data.
    - std_devs (np.ndarray): different standard deviation values for noise.
    - n_hids (np.ndarray): different values for hidden layer size.
    - n_hidden (int, default = 10): size of hidden layer.
    - n_reps (int, default = 100): number of resamples for data.
    - reg (float, default = 0): regularization constant.
    """
    with plt.xkcd():
        for sd in tqdm(std_devs):
            ###################################################################
            ## Fill out the following then remove
            raise NotImplementedError("Student exercise: complete calculation of mean test error for different noise values.")
            ###################################################################
            test_errs = [sweep_test(x_train, y_train + ..., x_test, y_test, n_hidden = n_hid, n_reps = n_reps, reg = reg * (1 + sd)) for n_hid in n_hids]
            plt.loglog(n_hids,test_errs,'o-',label="std={}".format(sd))

        plt.legend()
        plt.xlabel('Number of Hidden Units')
        plt.ylabel('Test Error')
        plt.show()

plot_error(x_train, y_train, x_test, y_test, std_devs, n_hids)

Click for solution

Example output:

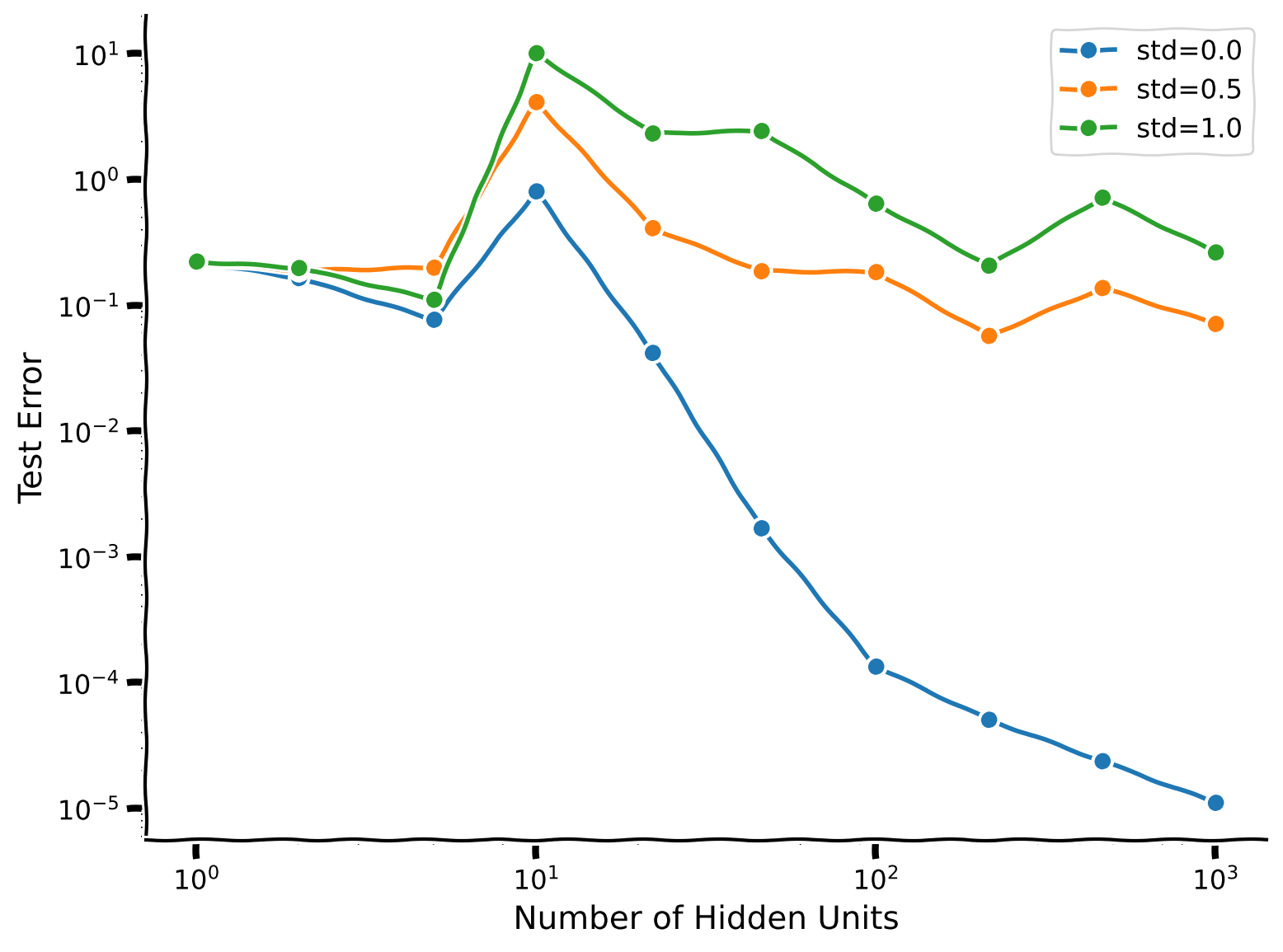
Though we are still able to observe the double descent effect, its strength is reduced with the increase in noise level.

Thus far, we have examined the impact of number of parameters without any explicit regularization (in which case we saw that all models with > 10 parameters fit all training data including noise). What happens if we add in explicit regularization to prevent overfitting? Let’s take a look. We’ll add L2 regularization to the weights of the network, also known as weight decay or Tikhonov regularization. The closed form solution for \(\mathbf{W}_2\) with L2 regularization is:

\[\mathbf{W}_2 = (\mathbf{H}^\top \mathbf{H} + \lambda \mathbf{I})^{-1} \mathbf{H}^\top \mathbf{y}\]

where \(\lambda\) is the regularization strength.

Observe the error plots with regularization term included#

We observe that the “peak” disappears, and the test error roughly monotonically decreases, although it is generally higher for higher noise levels in the training data.

The word regularization is commonly used in statistics/ML parlance in two different contexts to ensure the good generalization of overparameterized models:

The first context, which is emphasized throughout the tutorial, is explicit regularization which means that the model is not trained to completion (zero training error) in order to avoid overfitting of noise. Without explicit regularization, we observe the double descent behavior – i.e. catastrophic overfitting when the number of model parameters is too close to the number of training examples – but also a vast reduction in this overfitting effect as we heavily overparameterize the model. With explicit regularization (when tuned correctly), the double descent behavior disappears because we no longer run the risk of overfitting to noise at all.
The second context is the one of inductive bias – overparameterized models, when trained with popular optimization algorithms like gradient descent, tend to converge to a particularly “simple” solution that perfectly fits the data. By “simple”, we usually mean that the size of the parameters (in terms of magnitude) is very small. This inductive bias is a big reason why double descent occurs as well, in particular, the benefit of overparameterization in reducing overfitting.

When our training labels contain noise, are larger models still always better than smaller ones? You may have to run the cell a few times because even with 100 repetitions, these estimates can have high variance.

Edit the code below to visualize a 500-hidden unit network’s predictions for the case where the noise standard deviation is 0.2.

set_seed(42)

std_dev = .2

###################################################################
## Fill out the following then remove
raise NotImplementedError("Student exercise: complete noise calculation and add it in appropriate places.")
###################################################################

noise = np.random.normal(..., ..., y_train.shape)

n_hid = 500
n_reps = 10

with plt.xkcd():
    plt.plot(x_test, y_test,linewidth=4,label='Test data')
    plt.plot(x_train, y_train + ...,'o',label='Training data')
    train_err, test_err, y_pred = fit_relu(x_train, y_train + ..., x_test, y_test, n_hidden = n_hid)
    plt.plot(x_test, y_pred, color='g', label='Prediction')
    plt.legend()
    plt.xlabel('Input Feature')
    plt.ylabel('Target Output')
    plt.title('Number of Hidden Units = {}'.format(n_hid))
    plt.show()

Click for solution

Example output:

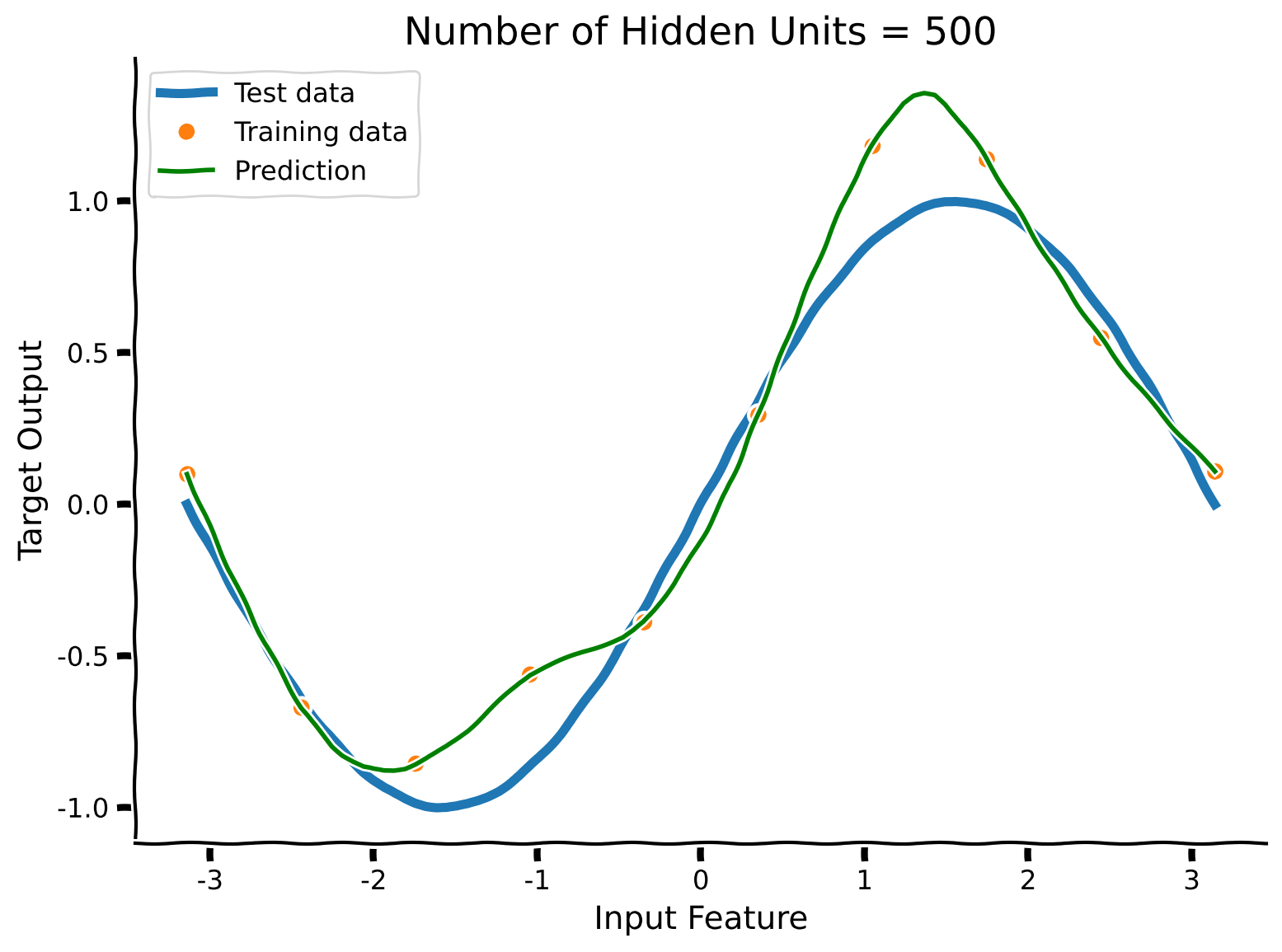
The network smoothly interpolates between the training datapoints. Even when noisy, these can still somewhat track the test data. Depending on the noise level, though, a smaller and more constrained model can be better.

From this, we might expect that large models will work particularly well for datasets with little label noise. Many real-world datasets fit this requirement: image classification datasets strive to have accurate labels for all datapoints, for instance. Other datasets may not. For instance, predicting DSM-V diagnoses from structural MRI data is a noisy task, as the diagnoses themselves are noisy.

Submit your feedback#

Section 4: Double descent and initialization#

Estimated timing to here from start of tutorial: 50 minutes

So far, we have considered one important aspect of architecture, namely the size or number of hidden neurons. A second critical aspect is initialization.

Video 5: Initialization Scale#

Submit your feedback#

Coding Exercise 5: Initialization scale impact#

Instead of initializing the second layer weights \(W_2\) to zero, we’ll now initialize them with i.i.d. Gaussian elements with a specified standard deviation.

Coding Exercise 5 Discussion#

How does this change the double descent curve?

Notice that executing this cell will take around 3 minutes. Thus, we invite you to guess / predict what you are going to see while the cell is running.

set_seed(42)
init_scales = np.linspace(0, 3, 5)

n_hids = np.unique(np.round(np.logspace(0, 3, 10))).astype(int)

###################################################################
## Fill out the following then remove
raise NotImplementedError("Student exercise: complete initial scale parameter assignment.")
###################################################################
with plt.xkcd():
    for sd in tqdm(init_scales):
        test_errs = [sweep_test_init_scale(x_train, y_train, x_test, y_test, init_scale = ..., n_hidden=n_hid, n_reps=100) for n_hid in n_hids]
        plt.loglog(n_hids,test_errs,'o-',label="Init Scale={}".format(sd))

    plt.legend()
    plt.xlabel('Number of Hidden Units')
    plt.ylabel('Test Error')
    plt.show()

Click for solution

Example output:

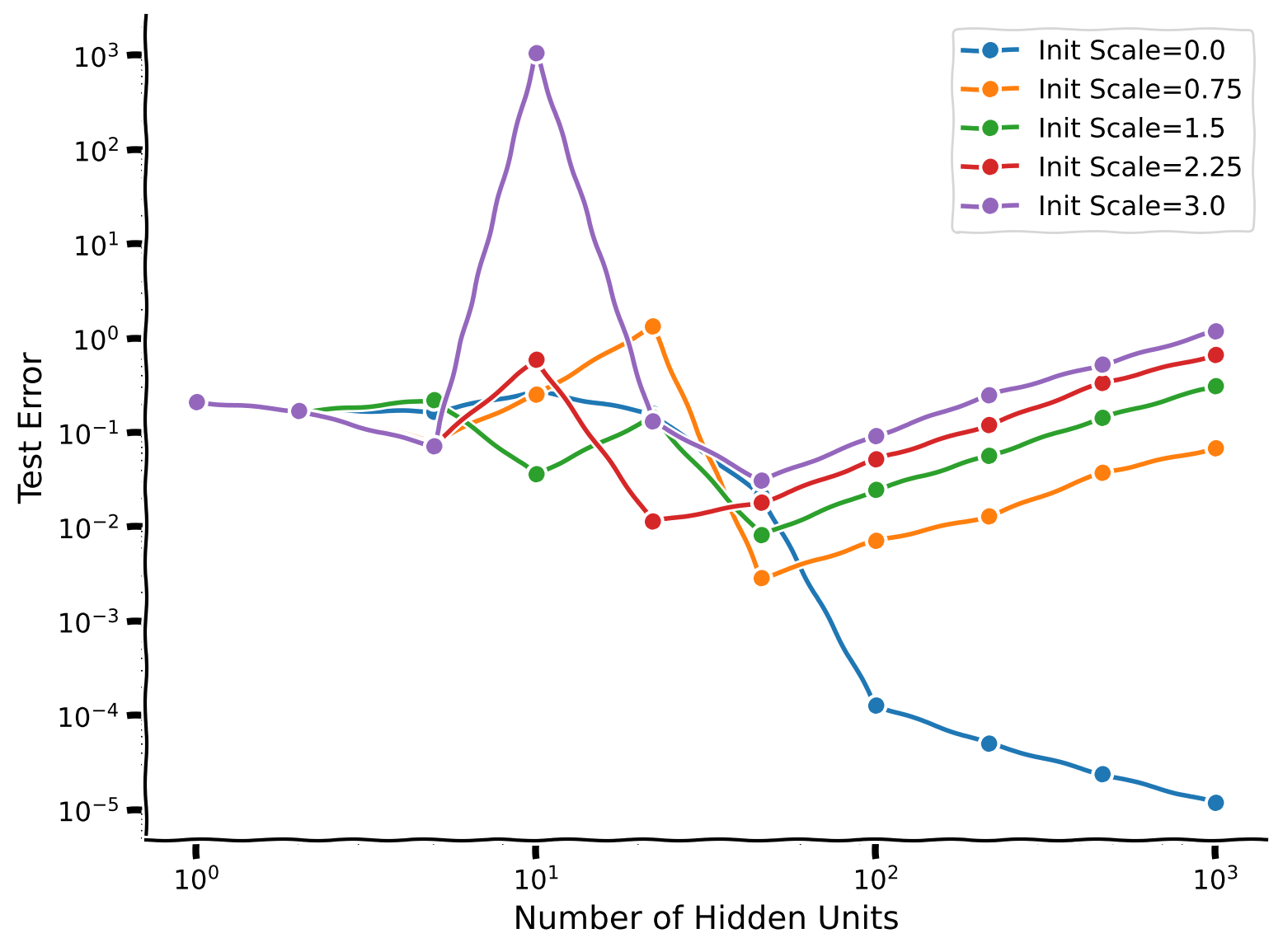
We see that for overparametrized models, where the number of parameters is larger than the number of training examples, the initialization scale strongly impacts the test error. The good performance of these large models thus depends on our choice of initializing \(W_2\) equal to zero.

Intuitively, this is because directions of weight space in which we have no training data are not changed by gradient descent, so poor initialization can continue to affect the model even after training. Large initializations implement random functions that generalize poorly.

Let’s see what the predictions of a large-variance-initialization network with 500 hidden neurons look like.

Execute the cell to observe the plot#

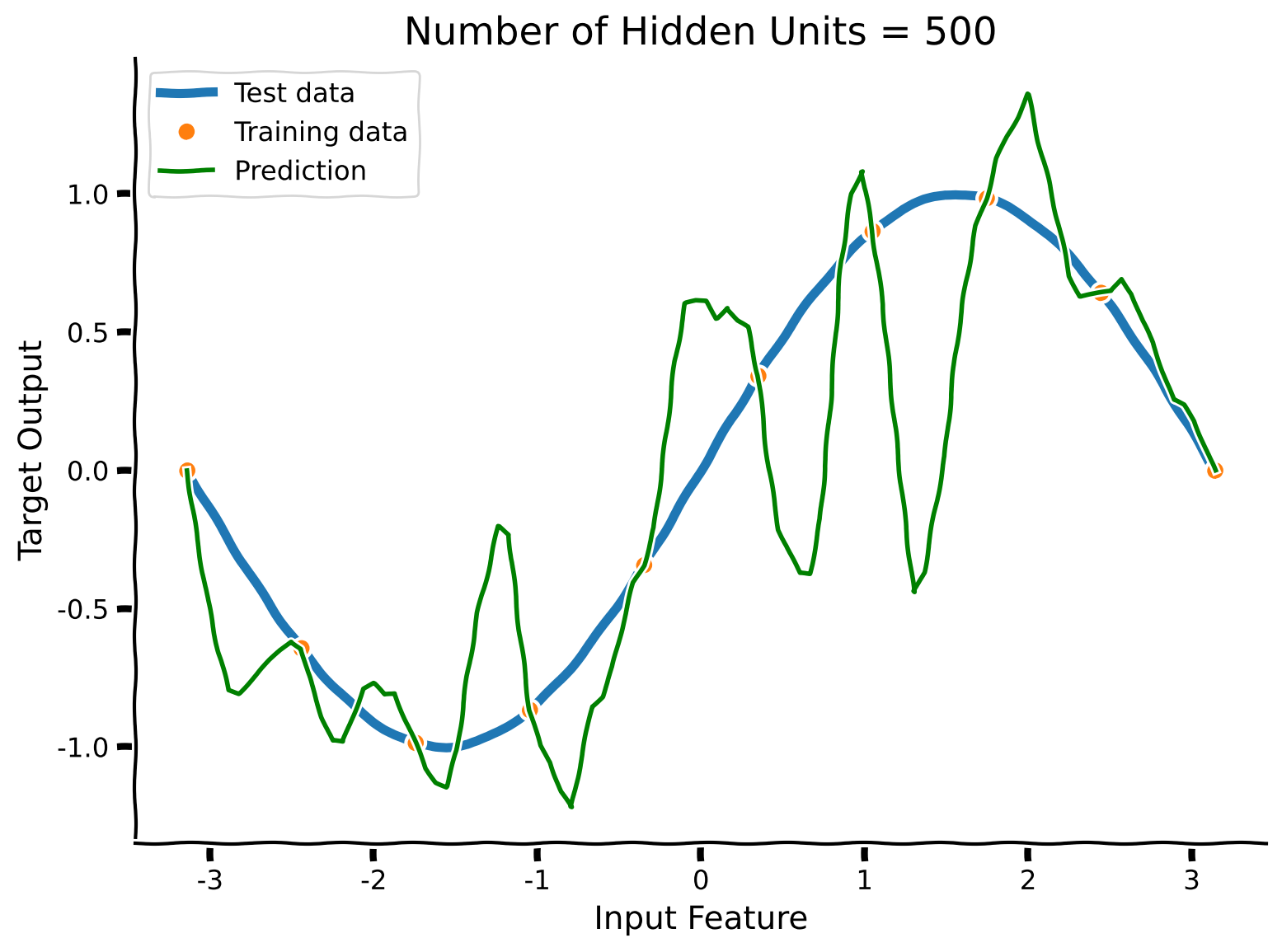
../../../_images/1bf6e109f86cd172ef7469bf763d7e25c4475bde705d2c6c5256606754a4c293.png

The network perfectly fits every training datapoint, but now connects them with more complex functions.

Intuitively, in a large network, there are many ways to achieve zero training error. Gradient descent tends to find solutions that are near the initialization. So simple initializations (here, small variance) yield less complex models that can generalize well.

Therefore, proper initialization is critical for good generalization in large networks.

There is one more mathematical trick to highlight, used in fit_relu_init_scale to find the appropriate weights. This passage is optional for those who would like to dive into implementation specifics.

Solution in case of non-zero weights initialization

The tutorial is trying to study what happens when you train the network with gradient descent for a very long time. However, if we actually trained these networks that way, it’d indeed take a very long time. So, we have picked a case where we know where training will end up and can calculate this endpoint in a different way. This case is basically a linear regression from the hidden layer activity. We have covered mathematical derivation at the very beginning of the tutorial.

Still, there’s one case that is a bit trickier: what if the network is overparametrized? That is, what if we have fewer data samples than weights? Then, there are many possible solutions that can result in zero training errors. Starting from some particular initialization \(w^0\), which one of these solutions will gradient descent end at? It turns out that the gradient descent dynamics only change the weights in the subspace spanned by the input training data. The component of the weights that start in the orthogonal complement of that subspace, the data null space, i.e., the subspace in which we have no data at all, doesn’t change at all during gradient descent learning. So, whatever initial values the weights take in that subspace will persist throughout training. To see this, note that the gradient update is \(\Delta w \propto \text{error} H^T\), so every update is in the direction of a training example. Therefore, to calculate \(w^{\text{gd}}\), the weights that gradient descent reaches convergence, we need to add the component of the weight initialization that lies in this data nullspace to the minimum norm linear regression solution given by the earlier equation for \(w\)^. That is, \(w^{gd} = w^ + (I-\text{pinv}(H)H)w^0\), where \(w^0\) is the initial weight vector and \((I-\text{pinv}(H)H)\) is one way of calculating the projection of that vector into the data nullspace.

To recap the intuition: shallow gradient descent learning in overparameterized models has a frozen subspace in which weight components do not change during learning, and so initial values in this subspace persist forever. We have to add the projection of our initialization on this frozen subspace to the minimum norm linear regression solution to obtain the solution that gradient descent would find. New test examples can then overlap with this frozen subspace, making the network’s test performance depend on the initial weights.

Submit your feedback#

Video 6: Summary#

Submit your feedback#

Summary#

Estimated timing of tutorial: 1 hour

In this tutorial, we observed the phenomenon of double descent: the situation when the overparameterized network was expected to behave as overfitted but instead generalized better to the unseen data. Moreover, we discovered how noise, regularization & initial scale impact the effect of double descent and, in some cases, can fully cancel it.

Combining with the findings from the first tutorial of the previous day on sparse connections and activity, brain architecture suggests it might operate in over parameterized regime, which enables the interpolation of vast amounts of sensory and experiential data smoothly, leading to effective generalization.

Tutorial 2: Double descent

Contents

Tutorial 2: Double descent#

Tutorial Objectives#

Setup#

Install and import feedback gadget#

Imports#

Figure settings#

Plotting functions#

Helper functions#

Set random seed#

Video 1: Introduction#

Submit your feedback#

Section 1: Overfitting in overparameterized models#

Video 2: Overfitting in Overparameterized Models#

Submit your feedback#

Coding Exercise 1: Learning with a simple neural network#

Sample and plot sinusoidal dataset#

Submit your feedback#

Coding Exercise 2: The bias-variance tradeoff#

Coding Exercise 2 Discussion#

Observe the performance on 5 hidden units#

Observe the performance on 10 hidden units#

Submit your feedback#

Section 2: The modern regime#

Video 3: Modern Regime#

Submit your feedback#

Observe the performance on 500 hidden units#

Coding Exercise 3: Observing double descent#

Interactive Demo 1: Interpolation point & predictions#

Execute this cell to observe interactive plot#

Submit your feedback#

Section 3: Double descent, noise & regularization#

Video 4: Noise & Regularization Effects#

Submit your feedback#

Coding Exercise 4: Noise & regularization impact#

Observe the error plots with regularization term included#

Submit your feedback#

Section 4: Double descent and initialization#

Video 5: Initialization Scale#

Submit your feedback#

Coding Exercise 5: Initialization scale impact#

Coding Exercise 5 Discussion#

Execute the cell to observe the plot#

Submit your feedback#

Video 6: Summary#

Submit your feedback#

Summary#